Computational Work in Science and Engineering
By Doris Hung
Computational research, as opposed to experimental research, uses mathematical and statistical models to simulate and make predictions for physical systems. Although modeling does not involve laboratory work, it follows the same procedures of planning, designing, performing modeling work, and analyzing the data as an experimentalist would do in the lab. The only difference is that the experiments are carried out with models on computers. Depending on the systems of interest being analyzed, there is usually more than one model available for researchers to use. Some models come from physical equations, and some are inferred by statistics. As famously stated by the statistician Dr. George Box, “All models are wrong, but some are useful.” A model can never make perfect predictions for the real-world, but if applied in suitable scenarios, models can provide meaningful insights in scientific research. It is the computational researchers’ responsibility to understand the derivation and constraints of different models and to know when to use one model over another. If conducted with appropriate judgements, computational work can replace expensive and time-consuming trial-and-error laboratory work or perceive system behaviors that are difficult to recreate with hands-on experiments.
Considerations when doing Computational Work
The implementation of a mathematical model on a computer often requires discretization and integration of continuous modeling equations. Commonly speaking, the finer the discretization resolution, the higher the model accuracy. Nonetheless, higher resolution models require more computing resources, and therefore it is the computational researchers’ job to determine the balance between accuracy and computing time. Another pitfall of computational work is misleading modeling results caused by non-realistic constraints. Many modeling software with more robust algorithms will generate results even when the boundary conditions or model setup are non-realistic. These types of misleading model results can lead to catastrophic consequences and are difficult to identify if the model setup is not well-documented. To prevent such issues, all decisions made in the process of building and using the model require well-justified rationales.
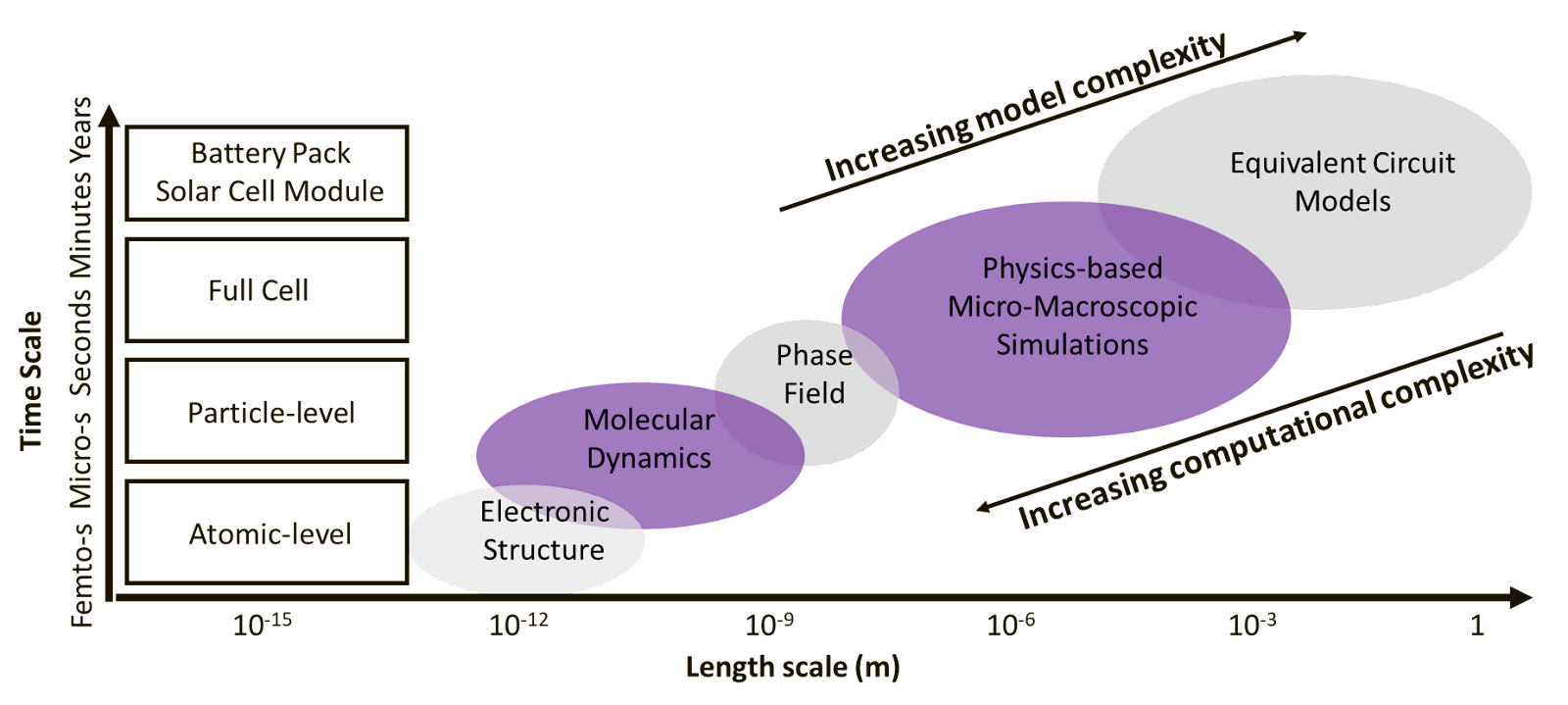
The Scale of Modeling in Batteries and Solar Cells
Batteries and solar cells are multi-scale systems, and different computational models are available at each scale. Take batteries for example, a single electrode-stack cell consists of an anode, a cathode, and a separator all immersed in liquid electrolyte and sandwiched between two current collectors. This single electrode-stack cell can further be stacked in layers and enclosed in packaging. Assemblies of battery cells wired together are called battery modules, and these modules together with the battery management systems form the battery pack found in electric vehicles. As shown in Figure 1, for scales larger than a single electrode battery cell, equivalent circuit models are often used. On the single electrode-stack level, physics-based models (see Figure 1) that describe the transport of ions and electrons in the electrodes are most applicable. For the length scale smaller than the size of the electrodes, there are micro-scale models such as the phase-field models that capture the evolution of particle boundaries or even models for molecular and atomic level interactions. Solar cell modeling follows the same general configuration with an extra layer of semiconductor absorber between anode and cathode to collect solar energy. The electronic properties of semiconductors and energy offsets between electrodes and absorbers are both critical for carrier transport and solar cell performance. Therefore, solar cell modeling generally focuses on bulk materials and junction areas.
Computational Research in 3D Electrode Architectures
Next-generation technologies such as all-electric vehicles and wearable devices require smaller, lighter, higher power, and higher energy batteries. Lithium-ion batteries (LIBs) are one of the most investigated materials due to their high energy and power densities. Conventional LIBs are manufactured by stacking and packaging multiple layers of planar electrode cells. Since all components are shaped as simple flat plates, these LIBs are referred to as 1D batteries. To increase the energy in 1D LIBs, it is essential to load as much active materials in the batteries as possible. A common approach is to increase the number of electrode cells. However, each extra electrode cell brings together an additional pair of current collectors. As the number of stacks increases, the heavy current collectors in the LIBs can occupy up to 50% of the weight and volume, which takes a toll on the energy density of the LIBs. Alternatively, we can increase the thicknesses of the planar electrodes to enable higher loadings of active materials without increasing the use of current collectors. Nevertheless, thick electrodes lengthen the Lithium-ion transport pathways in the cell, and therefore impair power performance.
Three-dimensional (3D) batteries decouple the power-energy trade-off in 1D LIBs by modifying the electrode architecture beyond planar form. Efficient manufacturing of 3D batteries is an active area of research and computational modeling is of paramount importance to define ideal 3D battery geometries before significant resources are invested into the development of new manufacturing methods and materials. In the Integrated Fabrication Lab, led by Dr. Corie L. Cobb, researchers investigate the use of pore channels in thick electrodes to enhance ion-transport in thick electrodes. With physics-based electrochemical models, the group analyze the effects of electrode thickness and geometry. Modeling estimations show that 3D electrodes can generate a >10% improvement in energy density over 1D LIB. Since the design space is large for 3D battery architectures, we continue to explore how 3D electrode spatial arrangement impacts energy and power performance in LIBs.
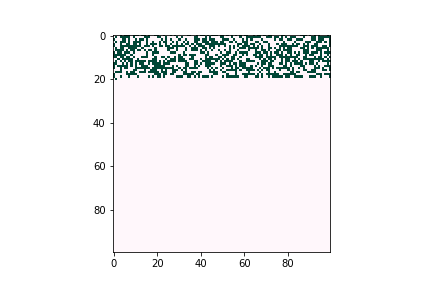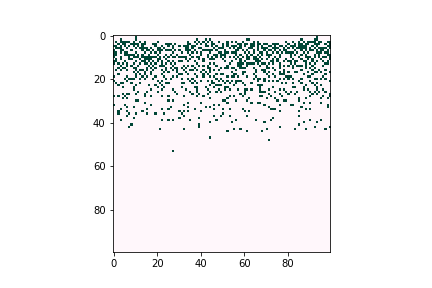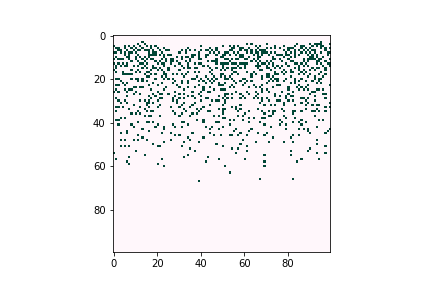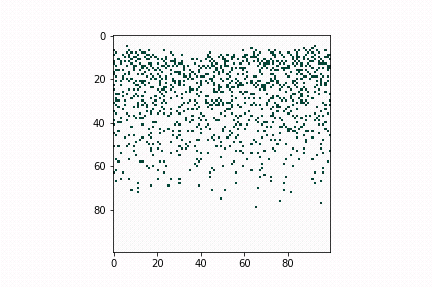
Computational Work in Diffusion in Solar Cells
The properties of solar cell absorbers, such as the Fermi level of minimum energy required to add an electron or the density of charge carriers, can be manipulated by adding “dopant” particles of a different element and controlling their density and depth. However, for a research lab or company, iterating through various levels of dopants would involve significant cost of time and resources. Therefore, computational models are used to simulate doping diffusion behavior in solar cells. In that way, scientists and engineers can predict how dopants diffuse into bulk films efficiently and accurately, enabling them to find an optimal elemental formula quickly and at low cost.
In the lab of UW electrical & computer engineering professor Scott Dunham, we develop defect diffusion and device performance models for chalcogenide solar cells to assist industry or academic research groups in designing the next generation of solar cells. In Figure 2, we use a kinetic Monte Carlo model to simulate dopant diffusion processes across bulk materials. The initial profile matches with pre-deposition of dopants. Diffusion energy barriers can be obtained through density functional theory or experimental data. The whole process is accelerated by kinetic Monte Carlo simulation.
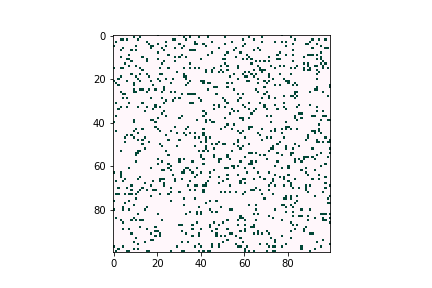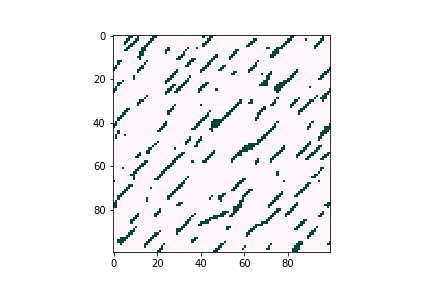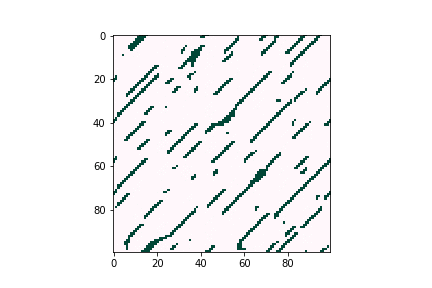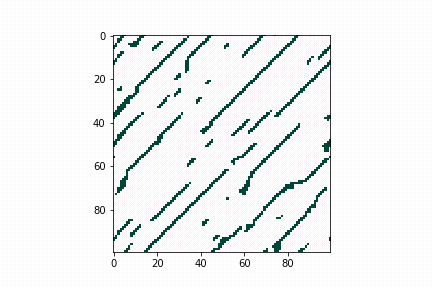
Defects can negatively affect solar cell performance, as they can often trap charge-carrying particles and thus deteriorate the overall efficiency of solar energy conversion. However, defects tend to be very dilute in the overall material composition, proving difficult to characterize experimentally. Computational tools are believed to be a good way to understand defect behavior as they can provide predictions even for trace concentrations of species, allowing researchers to optimize the composition and manufacturing conditions of their devices. Figure 3 illustrates how defects can form large clusters in bulk semiconductors and finally become voids, which are likely to become trap centers of carriers, which significantly reduce solar cell efficiencies.